How to choose a good model is always a big problem for machine learning technologies. I will show you simplicity is a practical guidance. Let’s begin with a simple problem. Here we have 10 data points^{Fig (a)}. Could you figure out a function which can fit these data points well and have the ability of predicting unseen data?

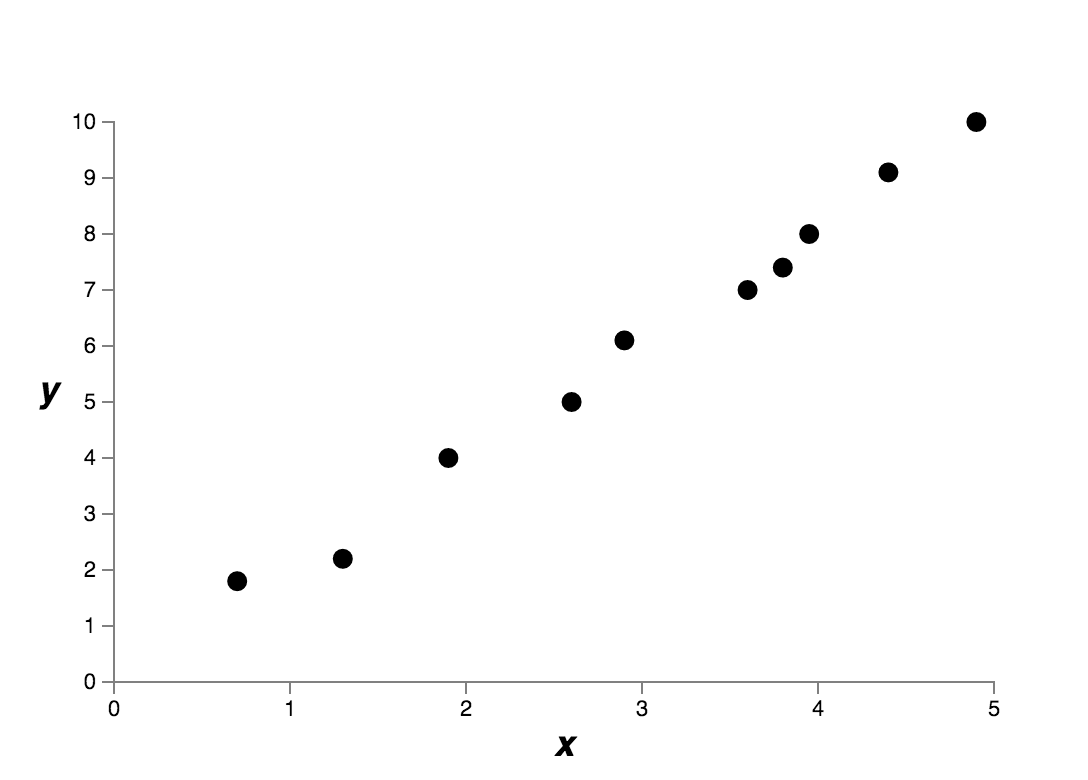
Fig (a) a regression problem

Well, a regression problem. As for this data set, we may find multiple models to fit it. Among them, the simplest model might be a linear model^{Fig (b)}. It may look like this. A much more complex model might be a 9th-order polynomial model^{Fig (c)} which fits the data set exactly like this. Here comes some questions. Which is the better model for this regression problem? Which model is more likely to generalize well to unseen data? Which model is more likely to be true?

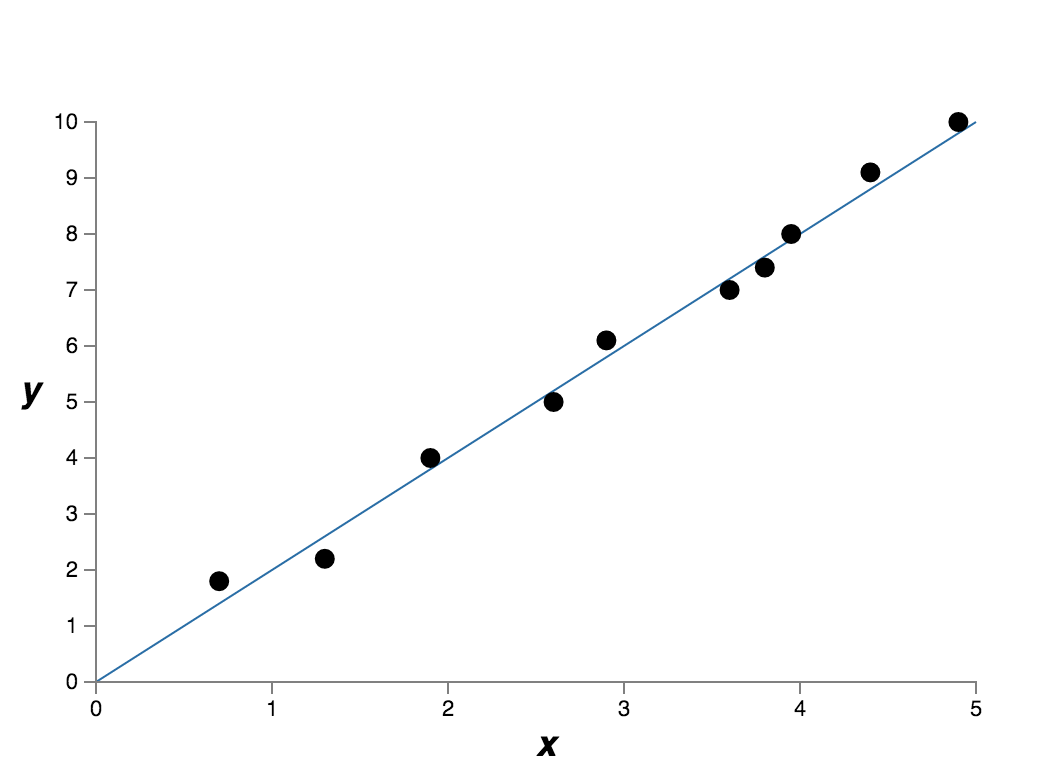
Fig (b) a simple model

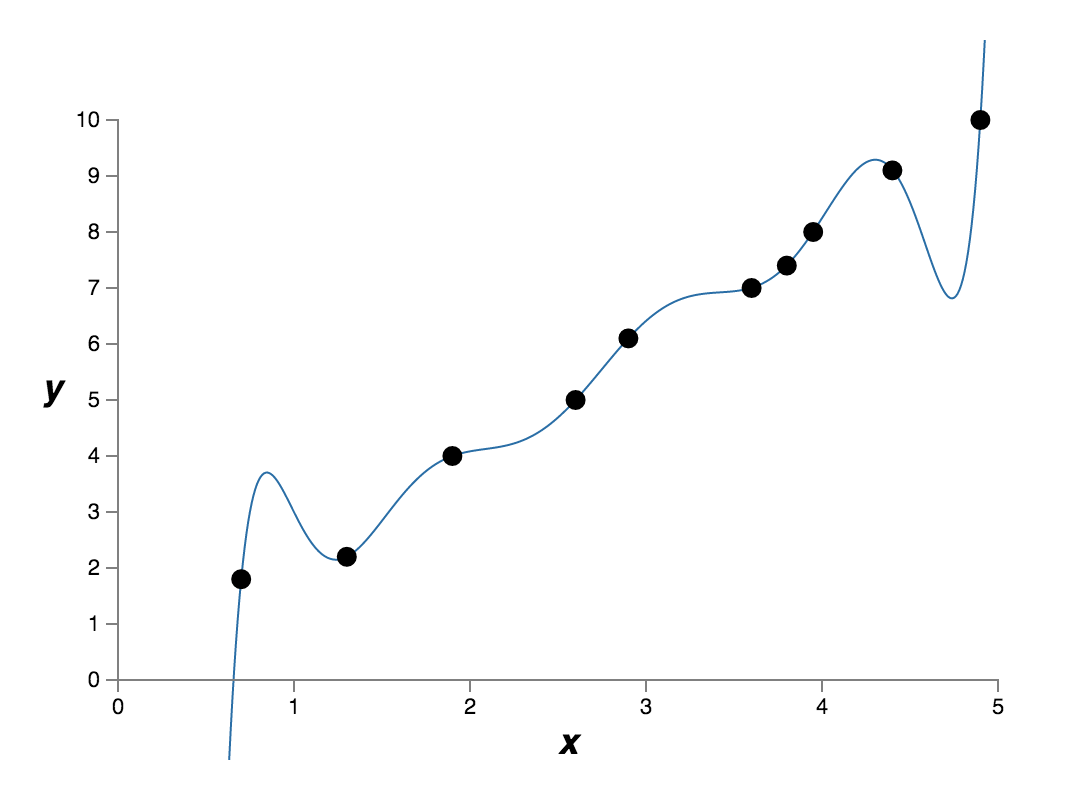
Fig (c) a complex model

Actually, we don’t know the exact answers. Without more information about the underlying real-world phenomenon, either model would be true. The 9th-order polynomial model fits the data set exactly, that’s good, while the linear model isn’t an exact fit probably because there is some random noise added to the data set, thus, essentially, the linear model might be a good enough model, too.

Well, either model would be true, that’s not good. Fortunately, there is a rule of thumb, not always right but quite useful. We prefer simple models than complex models. In other words, if a simple model can get the work done, we won’t bother to look for a complex model. We always start from a simple model. The idea behind it is a complex model is more likely to be overfitting which means it’s less likely to generalize well to unseen data. I remember Johnny von Neumann used to say, with four parameters I can fit an elephant, and with five I can make him wiggle his trunk. What he meant was it’s not surprising that a complex model can fit the data quite well. Just think about the 9th-order polynomial model I mentioned above, it can exactly fit the data set which has 10 data points. But that’s not surprising at all. We suspect this complex model is more likely to have trouble generalizing to unseen data. However, it’s surprising to us if a simple model can fit the data well because it’s not easy to occur by chance. We suspect this simple model might imply some essential ideas of the underlying real-world phenomenon thus it can generalize to unseen data well.

Again, not always right but quite useful. Start from a simple model. If it doesn’t generalize to unseen data well, then try some more complex models.

Last question, how to test whether a model generalizes well? There is a straightforward approach. Just split your data set into a training set and a validation set. Train you model on the training set, and validate its generalization performance on the validation set, then choose the model which is simple enough and does the work well.

Reference

[1] Neural Networks and Deep Learning - Improving the way neural networks learn